중위 표기법을 후위 표기법으로 변환하기
중위 표기법을 후위 표기법으로 바꿀 때는 다음의 절차를 따른다.
1) 피연산자가 들어오면 바로 출력한다.
2) 연산자가 들어오면 자기보다 우선순위가 높거나 같은 것들을 빼고 자신을 스택에 담는다.
3) 여는 괄호 '('를 만나면 무조건 스택에 담는다.
4) 닫는 괄호 ')'를 만나면 '('를 만날 때까지 스택에서 출력한다.
가장 중요한 것은 현재 처리중인 연산자와 스택에 있는 연산자의 우선순위를 이용한 처리 입니다.
1. 현재 처리 중인 연산자의 우선순위가 스택에 있는 연산자의 우선순위보다 낮을 때
예를들어) 처리중인 연산자: + or - , 스택에있는 연산자: * or / 일 때
=> 스택에 있는 연산자를 pop 해서 출력 후 처리 중인 연산자를 push 합니다.
2. 현재 처리 중인 연산자의 우선순위가 스택에 있는 연산자의 우선순위보다 클 때
예를들어) 처리중인 연산자: * or / , 스택에 있는 연산자: +, - 일 때
=> 현재 처리 중인 연산자를 그냥 push합니다.
3. 현재 처리중인 연산자의 우선순위와 스택에 있는 연산자의 우선순위가 같을 때
예를들어) 처리중인 연산자: +, 스택에 있는 연산자: - 일 때
=> 1번 경우와 똑같이 처리한다.
후위 표기법을 계산하기
후위 표기법을 계산할 때는 다음의 절차를 따른다.
1) 피연산자를 만나면 스택에 담는다.
2) 연산자를 만나면 스택에서 두 개의 연산자를 꺼내서 연산한 뒤에 그 결과를 스택에 담는다.
3) 연산을 마치고 스택에 남아있는 하나의 피연산자가 연산 수행 결과이다.

아래 코드는 중위 표기법으로 변환하는 코드 및 익셉션 체크도 함께 해주는 코드이다.
해당 글은 아래 코드를 좀 더 상세히 적은 글이다
typedef struct {
element data[MAX_STACK_SIZE];
int top;
} StackType;
element : typedef로 선언된 char type, 이는 가독성을 늘리기 위해 사용된다.
element data[MAX_STACK_SIZE] : element data 배열, 이는 MAX_STACK_SIZE(현재 100으로 설정)만큼 크기의 배열을 가지고 있게 된다.
top : 현재 stack의 가장 윗부분을 인덱스로 나타내고 있다.
* infix_to_postfix 함수에서
element* postfix_arr = (element*)malloc(MAX_STACK_SIZE); 라는 포인터가 있는데
이는 후위 표기법으로 변환된 결과물을 담을 배열이 된다.
알고리즘
중위 표기식을 후위 표기식으로 바꾸는 과정은 다음과 같다.
1. 0~9사이 숫자가 들어오면 postfix_arr에 넣어준다.
2. 현재 문자가 ‘(’ 라면 스택에 ‘(’ 를 넣어준다. 이는 추후에 ‘)’가 들어왔을 때 ‘(’가 어디까지 있는지 확인하기 위해 스택에 넣어두는 것이다.
3. 현재 문자가 ‘)’라면 스택에서 ‘(’가 나타날 때 까지 모든 내용을 postfix_arr에 담는다. 이때 ‘(’와 ‘)’는 따로 담지 않는다.
4. 현재 문자가 연산자(‘+’,‘-’,‘*’,‘/’)라면 우선 순위를 정한다. 이때 현재 연산자보다 스택에 존재하는연산자가 우선순위가 더 높다면 postfix_arr에 담아준다. 계속 반복하여 현재 연산자가 우선순위가 높은 상황이 되면 자기 자신을 스택에 넣어준다.
Main문
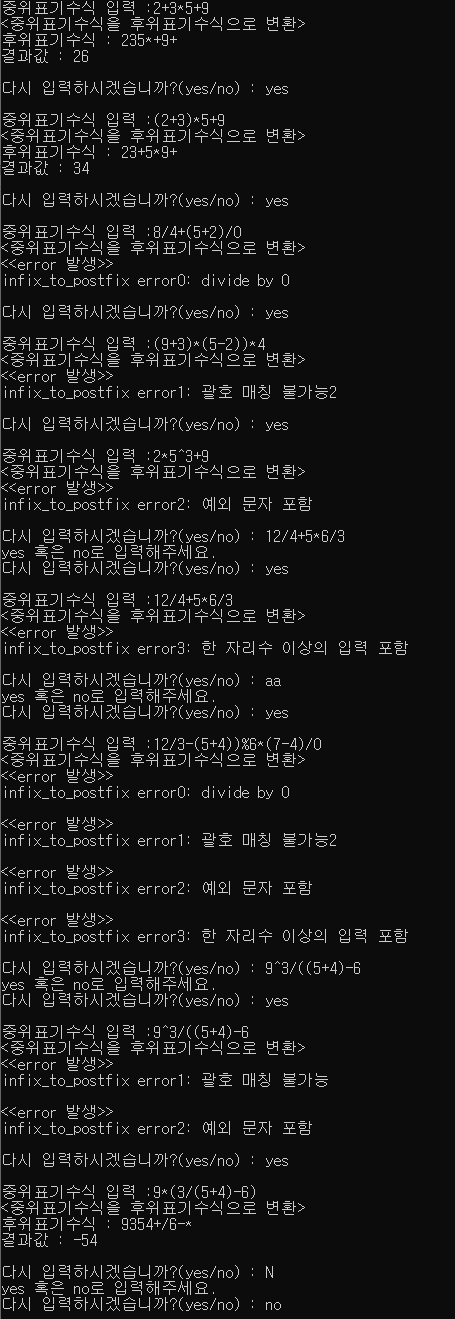
무한 반복문을 통해 중위 표기식을 입력받는다. 이때 infix_to_postfix 함수를 통해 후위 표기수식으로 변환을 해줄 수 있다.
만약 후위 표기식 변환 도중에 에러가 발생하지 않는다면 (err == -1) 후위 표기 수식과 결과값을 출력해준다.
이후 다시 입력할지 여부에 대해 검사하고 yes면 다시 no면 종료 이외의 문자는 계속 입력받도록한다.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_STACK_SIZE 100
int err = 0; //에러가 발생했는지 체크하는 변수(0: 에러 없음, 1: 에러 발생)
typedef char element;
// ===== 스택 코드의 시작 =====
typedef struct {
element data[MAX_STACK_SIZE];
int top;
} StackType;
// 스택 초기화 함수
void init_stack(StackType *s)
{
s->top = -1;
}
// 공백 상태 검출 함수
int is_empty(StackType *s)
{
return (s->top == -1);
}
// 포화 상태 검출 함수
int is_full(StackType *s)
{
return (s->top == (MAX_STACK_SIZE - 1));
}
// 삽입함수
void push(StackType *s, element item)
{
if (is_full(s)) {
fprintf(stderr, "스택 포화 에러\n");
return;
}
else s->data[++(s->top)] = item;
}
// 삭제함수
element pop(StackType *s)
{
if (is_empty(s)) {
fprintf(stderr, "스택 공백 에러\n");
exit(1);
}
else return s->data[(s->top)--];
}
// 피크함수
element peek(StackType *s)
{
if (is_empty(s)) {
fprintf(stderr, "스택 공백 에러\n");
exit(1);
}
else return s->data[s->top];
}
// ===== 스택 코드의 끝 =====
// 후위 표기 수식 계산 함수
int eval(char exp[])
{
int op1, op2, value, i = 0;
int len = strlen(exp);
char ch;
StackType s;
init_stack(&s);
for (i = 0; i < len; i++) {
ch = exp[i];
if (ch != '+' && ch != '-' && ch != '*' && ch != '/') {
value = ch - '0'; // 입력이 피연산자이면
push(&s, value);
}
else { //연산자이면 피연산자를 스택에서 제거
op2 = pop(&s);
op1 = pop(&s);
switch (ch) { //연산을 수행하고 스택에 저장
case '+': push(&s, op1 + op2); break;
case '-': push(&s, op1 - op2); break;
case '*': push(&s, op1 * op2); break;
case '/': push(&s, op1 / op2); break;
}
}
}
return pop(&s);
}
// 연산자의 우선순위를 반환한다.
int prec(char op)
{
switch (op) {
case '(': case ')': return 0;
case '+': case '-': return 1;
case '*': case '/': return 2;
}
return -1;
}
void check_error(element exp[]) {
err = -1;
int len = strlen(exp);
// error 0 : / 연산자 후 0이 오면 예외처리
for (int i = 0; i < len; i++) {
if (i + 1 < len && exp[i] == '/' && exp[i + 1] == '0') {
printf("<<error 발생>>\n");
printf("infix_to_postfix error0: divide by 0\n\n");
err = 0;
break;
}
}
int count = 0;
// error 1 : 괄호의 짝이 맞지 않으면 예외처리
for (int i = 0; i < len; i++) {
if (exp[i] == '(') {
count++;
}
else if (exp[i] == ')') {
count--;
}
}
if (count > 0) {
printf("<<error 발생>>\n");
printf("infix_to_postfix error1: 괄호 매칭 불가능\n\n");
err = 1;
}
else if (count < 0) {
printf("<<error 발생>>\n");
printf("infix_to_postfix error1: 괄호 매칭 불가능2\n\n");
err = 1;
}
// error 2 : 예외 문자 포함
for (int i = 0; i < len; i++) {
if (exp[i] == '(' || exp[i] == ')') {
continue;
}
else if (exp[i] == '+' || exp[i] == '-' || exp[i] == '*' || exp[i] == '/') {
continue;
}
else if ('0' <= exp[i] && exp[i] <= '9') {
continue;
}
else {
printf("<<error 발생>>\n");
printf("infix_to_postfix error2: 예외 문자 포함\n\n");
err = 2;
}
}
// error 3 : 한 자리 수 이상의 수 입력에 대해 예외 처리(예시: 23, 123, ...)
int count_len = 0;
int max_len = 0;
for (int i = 0; i < len; i++) {
if ('0' <= exp[i] && exp[i] <= '9') {
count_len++;
if (count_len >= max_len) {
max_len = count_len;
}
}
else {
count_len = 0;
}
}
if (max_len >= 2) {
printf("<<error 발생>>\n");
printf("infix_to_postfix error3: 한 자리수 이상의 입력 포함\n\n");
err = 3;
}
}
// 수식 변환함수
element* infix_to_postfix(element exp[])
{
// 입력받은 표기식 에러 검사
check_error(exp);
// 에러가 있다면 다시 실행
if (err != -1) {
return NULL;
}
int i, idx = 0; //i는 for문의 제어변수, idx는 post_arr의 index
int len = strlen(exp);
char ch, op;
StackType s;
element* postfix_arr = (element*)malloc(MAX_STACK_SIZE);
if (postfix_arr == NULL) {
fprintf(stderr, "메모리 할당 에러\n");
exit(1);
}
init_stack(&s); //스택 초기화
// 중위 표기식으로 표현된 식을 순회
for (int i = 0; i < len; i++)
{
// 값을 뽑는다
ch = exp[i];
// 일반 숫자라면 그대로 postfix_arr에 추가
if ('0' <= ch && ch <= '9') {
postfix_arr[idx++] = ch;
}
// 연산자 +,-,*,/라면
else if (ch == '+' || ch == '-' || ch == '*' || ch == '/') {
// 스택의 top 값이 현재 연산자보다 우선순위가 높다면
while (!is_empty(&s) && (prec(ch) <= prec(peek(&s))))
{
// 해당 값들은 모두 추가해준다.
postfix_arr[idx++] = peek(&s);
pop(&s);
}
// 자기자신을 스택에 추가한다.
push(&s, ch);
}
// '('는 무조건 스택에 추가한다.
else if (ch == '(') {
push(&s, ch);
}
// ')'가 나오면 '('가 나올때 까지 스택에서 pop하여 추가해준다.
else if (ch == ')') {
op = pop(&s);
while (op != '(')
{
postfix_arr[idx++] = op;
op = pop(&s);
}
}
}
//아직 스택에 남아있는 값들을 모두 추가해준다.
while (!is_empty(&s)) {
op = peek(&s);
pop(&s);
postfix_arr[idx++] = op;
}
// 문자열의 끝을 지정해준다.
postfix_arr[idx] = '\0';
return postfix_arr;
}
int main(void)
{
element expression[MAX_STACK_SIZE];
char word[100];
// 무한 반복문
while (1) {
// 중위 표기식 입력
printf("중위표기수식 입력 :");
scanf("%s", expression);
// 중위 표기식 및 결과 값 표시
printf("<중위표기수식을 후위표기수식으로 변환>\n");
element *result = infix_to_postfix(expression);
if (err == -1) {
printf("후위표기수식 : %s\n", result);
printf("결과값 : %d\n\n", eval(result));
}
// 다시 입력할지 여부 검사
int exit = 0;
while (1) {
printf("다시 입력하시겠습니까?(yes/no) : ");
scanf("%s", word);
// yes면 다시 시작
if (strcmp(word, "yes") == 0) {
break;
}
// no 면 exit = 1로 값 설정
else if (strcmp(word, "no") == 0) {
exit = 1;
break;
}
// 이외 값은 yes, no중 입력 들어오도록 while문 다시 시작
else {
printf("yes 혹은 no로 입력해주세요.\n");
continue;
}
}
// exit가 1이면 (no입력시) break를 통해 종료
if (exit == 1) {
break;
}
else {
printf("\n");
}
}
return 0;
}
'Applied > 알고리즘' 카테고리의 다른 글
| 2차원 좌표 차원축소 알고리즘 (0) | 2024.02.28 |
|---|---|
| 수학 공식 일반화 유틸 (Mathemetic utility) (0) | 2020.01.01 |
| 시계방향, 반시계 방향 좌표 정렬 (0) | 2019.12.31 |
| 다각형 내부 외부 판별 알고리즘 (0) | 2019.11.15 |
| 힙(Heap) 좀더 깔끔하게 짠 코드 (0) | 2019.07.19 |